2. Stereonetz¶
Stereonetze oder Stereographische Projektionen (auch Lagenkugel und Lagenkugelprojektion) sind eine der wichtigsten Darstellungsarten für raumbezogene Daten in der Strukturgeologie. Ihr Vorteil liegt darin, dass jede beliebige Orientierung im Raum in einer Ebene dargestellt werden kann. Am häufigsten wird dabei die flächentreue Projektion verwendet.
In der Geologie verwendet man zumeist die Einfallrichtung und das Einfallen um eine Struktur zu erfassen. Diese beiden Angabe in belieber Reihenfolge, reichen aus um eine Struktur in ihrer räumlichen Lage zu beschreiben. Die Einfallrichtung wird relativ zum geographischen Nordpol bestimmt, wobei die Winkel im Uhrzeigersinn ansteigen. Das Einfallen ist ein Tiefenwinkel, der relativ zur Horizontalebene nach unten gemessen wird. Beide Werte lassen sich mit einem Geologenkompass in einem Arbeitsschritt bestimmen.
Die Einfallrichtung wird immer mit drei Stellen angegeben, um sie vom zweistelligen Einfallen zu unterscheiden. Eine Lage einer Struktur die nach Osten mit 45° einfällt kann deswegen entweder mit 090/45 oder mit 45/090 eindeutig beschrieben werden. Für Strukturen die eine Richtung haben (z.B. Strömungsrichtung einer sedimentären Struktur) oder eine Magnitude haben (z.B. ein Versatz) müssen zusätzliche Angaben notiert werden.
2.1. Projektionen¶
2.1.1. Flächentreue-Projektion¶
Für die meisten Fragestellungen in der Geologie ist es von Vorteil eine räumlich gleichmäßige Datenverteilung zu betrachten. Die dafür geeignetste Projektion ist die flächentreue Azimutalprojektion (oder Lambert’sche Azimutalprojektion). In der Geologie spricht man auch vom Schmidt’schen Netz (benannt nach Walter Schmidt).
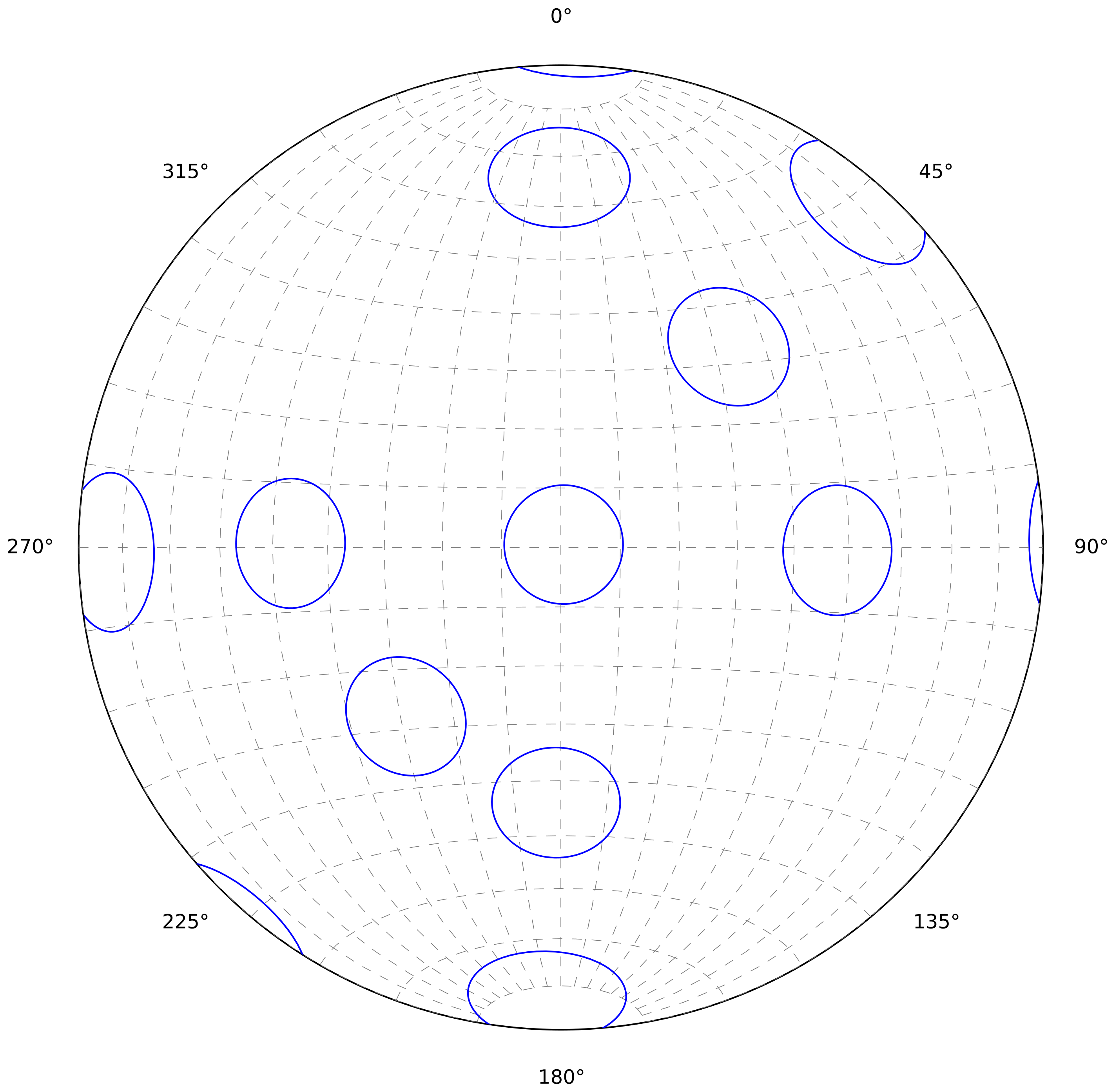
Diese Abbildung zeigt eine Reihe von Kleinkreisen mit einem Radius von 10°. Die Größe der Kreise bleibt über den gesamten Bereich relativ gut erhalten, während aufgrund der Winkelverzerrung die Kreise gegen den Rand hin zu Ellipsen verzerrt werden.
2.1.1.1. Transformation¶
Aus einer Messung von Längen- und Breitengraden berechnen sich die X- und Y-Koordinaten der äquatorialen Lambert-Projektion aus folgenden Formeln (Snyder 1987):
Mit k gleich:
Die Variablen stehen für:
- R … Radius
- ϕ … Breitengrad
- λ … Längengrad
- λ₀ … Zentralmeridian (y-Achse)
Die inverse Transformation, berechnet aus den XY-Koordinaten die Längen- und Breitengrade:
Für den Längengrad wird abhängig vom Breitengrad eine dieser drei Formeln verwedent:
Für Φ₁ gleich +90°:
Für Φ₁ gleich -90°:
Für alle anderen Breitengrade verwendet man:
Dabei gilt:
2.1.2. Winkeltreue-Projektion¶
2.2. Literatur¶
- John P. Snyder (1987): Map Projections - A Working Manual
- Flächentreue Azimutalprojektion auf Wikipedia
- Schmidt’sches Netz auf Wikipedia
- Wulff’sches Netz auf Wikipedia
- Georgij Viktorovich Wulff auf Wikidata
- Walter Schmidt auf Wikidata
